数据结构_8

发表于
字数统计 1.3k | 阅读时长 5

学习过程主要依照中国MOOC课程，感谢MOOC，感谢浙大授课大佬。
这里只讨论内部排序，即默认内存空间足够大，可以存放下所有需要排序的数据。

简单排序（冒泡、插入）

冒泡排序

从上到下比较两个相邻的泡泡，小在上，大在下则不动，否则交换顺序。这为第一趟冒泡，保证将最大的元素放到最下边，然后重复冒泡，直到所有元素均排好序。
最好情况：顺序T=O(N)
最坏情况：倒序T=O(N2)

插入排序

类比于打牌时抓牌的过程。
最好情况：顺序T=O(N)
最坏情况：倒序T=O(N2)

1
2
3
4
5
6
7
8
9
10
11
12
void InsertionSort( ElementType A[], int N )
{ /* 插入排序 */
     int P, i;
     ElementType Tmp;
      
     for ( P=1; P<N; P++ ) {
         Tmp = A[P]; /* 取出未排序序列中的第一个元素*/
         for ( i=P; i>0 && A[i-1]>Tmp; i-- )
             A[i] = A[i-1]; /*依次与已排序序列中元素比较并右移*/
         A[i] = Tmp; /* 放进合适的位置 */
     }
}

时间复杂度下界

对于下标i<j，如果A[i]>A[j]，则称（i,j）是一对逆序对。
冒泡排序和插入排序中需要交换的次数即逆序对数，也就是每次交换消除一个逆序对。

希尔排序

希尔排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
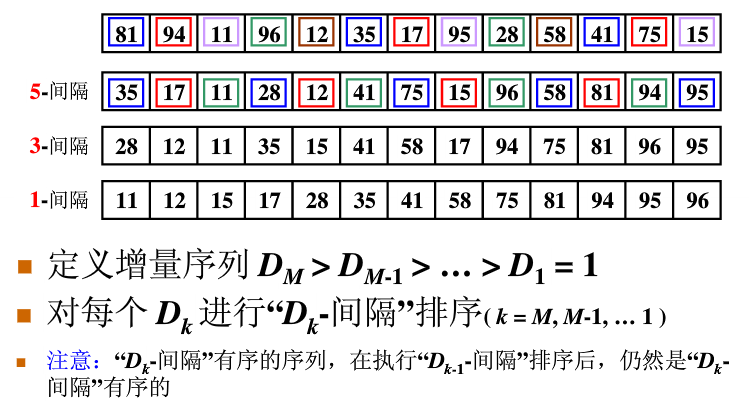
void ShellSort( ElementType A[], int N )
{ /* 希尔排序 - 用Sedgewick增量序列 */
     int Si, D, P, i;
     ElementType Tmp;
     /* 这里只列出一小部分增量 */
     int Sedgewick[] = {929, 505, 209, 109, 41, 19, 5, 1, 0};
      
     for ( Si=0; Sedgewick[Si]>=N; Si++ ) 
         ; /* 初始的增量Sedgewick[Si]不能超过待排序列长度 */
 
     for ( D=Sedgewick[Si]; D>0; D=Sedgewick[++Si] )
         for ( P=D; P<N; P++ ) { /* 插入排序*/
             Tmp = A[P];
             for ( i=P; i>=D && A[i-D]>Tmp; i-=D )
                 A[i] = A[i-D];
             A[i] = Tmp;
         }
}

堆排序

选择排序

在i从0到N的循环里，从A[i]到A[i-1]中找到最小元，并将其位置赋给MinPostion，将未排序部分的最小元换到有序部分的最后位置，即交换A[i]和A[MinPostion]。

堆排序

将找最小元用最小堆来解决。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
void Swap( ElementType *a, ElementType *b )
{
     ElementType t = *a; *a = *b; *b = t;
}
  
void PercDown( ElementType A[], int p, int N )
{ /* 改编代码4.24的PercDown( MaxHeap H, int p )    */
  /* 将N个元素的数组中以A[p]为根的子堆调整为最大堆 */
    int Parent, Child;
    ElementType X;
 
    X = A[p]; /* 取出根结点存放的值 */
    for( Parent=p; (Parent*2+1)<N; Parent=Child ) {
        Child = Parent * 2 + 1;
        if( (Child!=N-1) && (A[Child]<A[Child+1]) )
            Child++;  /* Child指向左右子结点的较大者 */
        if( X >= A[Child] ) break; /* 找到了合适位置 */
        else  /* 下滤X */
            A[Parent] = A[Child];
    }
    A[Parent] = X;
}
 
void HeapSort( ElementType A[], int N ) 
{ /* 堆排序 */
     int i;
       
     for ( i=N/2-1; i>=0; i-- )/* 建立最大堆 */
         PercDown( A, i, N );
      
     for ( i=N-1; i>0; i-- ) {
         /* 删除最大堆顶 */
         Swap( &A[0], &A[i] ); /* 见代码7.1 */
         PercDown( A, 0, i );
     }
}

归并排序

核心：有序子列的归并

递归算法

分而治之，T(N)=O(NlogN)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/* 归并排序 - 递归实现 */
 
/* L = 左边起始位置, R = 右边起始位置, RightEnd = 右边终点位置*/
void Merge( ElementType A[], ElementType TmpA[], int L, int R, int RightEnd )
{ /* 将有序的A[L]~A[R-1]和A[R]~A[RightEnd]归并成一个有序序列 */
     int LeftEnd, NumElements, Tmp;
     int i;
      
     LeftEnd = R - 1; /* 左边终点位置 */
     Tmp = L;         /* 有序序列的起始位置 */
     NumElements = RightEnd - L + 1;
      
     while( L <= LeftEnd && R <= RightEnd ) {
         if ( A[L] <= A[R] )
             TmpA[Tmp++] = A[L++]; /* 将左边元素复制到TmpA */
         else
             TmpA[Tmp++] = A[R++]; /* 将右边元素复制到TmpA */
     }
 
     while( L <= LeftEnd )
         TmpA[Tmp++] = A[L++]; /* 直接复制左边剩下的 */
     while( R <= RightEnd )
         TmpA[Tmp++] = A[R++]; /* 直接复制右边剩下的 */
          
     for( i = 0; i < NumElements; i++, RightEnd -- )
         A[RightEnd] = TmpA[RightEnd]; /* 将有序的TmpA[]复制回A[] */
}
 
void Msort( ElementType A[], ElementType TmpA[], int L, int RightEnd )
{ /* 核心递归排序函数 */ 
     int Center;
      
     if ( L < RightEnd ) {
          Center = (L+RightEnd) / 2;
          Msort( A, TmpA, L, Center );              /* 递归解决左边 */ 
          Msort( A, TmpA, Center+1, RightEnd );     /* 递归解决右边 */  
          Merge( A, TmpA, L, Center+1, RightEnd );  /* 合并两段有序序列 */ 
     }
}
 
void MergeSort( ElementType A[], int N )
{ /* 归并排序 */
     ElementType *TmpA;
     TmpA = (ElementType *)malloc(N*sizeof(ElementType));
      
     if ( TmpA != NULL ) {
          Msort( A, TmpA, 0, N-1 );
          free( TmpA );
     }
     else printf( "空间不足" );
}

非递归算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/* 归并排序 - 循环实现 */
/* 这里Merge函数在递归版本中给出 */
 
/* length = 当前有序子列的长度*/
void Merge_pass( ElementType A[], ElementType TmpA[], int N, int length )
{ /* 两两归并相邻有序子列 */
     int i, j;
       
     for ( i=0; i <= N-2*length; i += 2*length )
         Merge( A, TmpA, i, i+length, i+2*length-1 );
     if ( i+length < N ) /* 归并最后2个子列*/
         Merge( A, TmpA, i, i+length, N-1);
     else /* 最后只剩1个子列*/
         for ( j = i; j < N; j++ ) TmpA[j] = A[j];
}
 
void Merge_Sort( ElementType A[], int N )
{ 
     int length; 
     ElementType *TmpA;
      
     length = 1; /* 初始化子序列长度*/
     TmpA = malloc( N * sizeof( ElementType ) );
     if ( TmpA != NULL ) {
          while( length < N ) {
              Merge_pass( A, TmpA, N, length );
              length *= 2;
              Merge_pass( TmpA, A, N, length );
              length *= 2;
          }
          free( TmpA );
     }
     else printf( "空间不足" );
}

以上。

注：转载文章请注明出处，谢谢~